Instructions :-

1. Conventions regarding decision variables in line/circle/ellipse drawing algorithms, clipping, area filling have to be STRICTLY followed as taken up by the instructor in the class.
2. Improper/incomplete/half-done calculations/derivations will not get any credit.

1. Give Global Edge Table (GET) and Active Edge List (AEL) for the scanlines no. 1, 2, 5, 7 and 8 for the polygon defined on the screen by

   (2,2) - (6,1) - (6,5) - (8,5) - (8,8) - (4,8) - (2,2)

   Show only those edges in AEL that are used in span calculation for that scan line. Marks shall not be given if you show extra edges in AEL. Also, give well labelled pictorial data structure of the node in AEL/GET, that you have used in your answer.
2. Give short/precise answers for the following -
   
   
   1. Which rule - odd-even or non-zero winding number, will you make use of to implement area filling of character outlines. Justify with the help of suitable example.
   2. Give the transformation matrix for scaling a tetrahedron by Sx, Sy and Sz along X,Y and Z axis respectively, such that the centroid of the tetrahedron stays at same point (Xc, Yc, Zc). Explain, how you obtained the transformation matrix.
   3. Give the transformation matrix for shearing along any arbitrary line "A * y = B * x + C" (where A, B, C are integer values) in XY plane. Explain, how you obtained the transformation matrix.
3. How will you scan convert a parabola "A * y = B * x^2 + C'' (where A, B, C are integer values) using Bresenham's approach. Discuss various issues involved like - derivation of decision variables, their initial values, choices of pixel to light up based on decision variables etc. as discussed in the class for various line/circle/ellipse drawing algorithms. OR Given the screen coordinates of a line as (10,20) - (95,30), give the pixel coordinates for the values of x in closed interval I1i and I2 for this line, using Bresenham's line drawing algorithm, where -

   i = your-roll-number mod 4
   I10 = 25 to 27 , I11 = 40 to 42 , I12 = 55 to 57 , I13 = 70 to 72
   I2 = 85 to 87

   In each of the cases, give decision variable's value at all the pixels corresponding to x values in the interval. Also label the selected pixels as NE/N/E wrt to previous one selected, except for the start point in each case. Adapt the Bresenham algorithm to obtain the pixels with minimal computations. Give logic/derivations used in solving this problem.
4. Given the convex polygon "(15,15) - (35,15) - (15,30) - (15,15)", clip the line segments Li and Lk against this using Cyrus-Beck line clipping algorithm, where -

   i = your-Roll-No mod 4 , k = (your-Roll-No + 1) mod 4
   L0 : (5,13) - (60,20) L1 : (22,20) - (24,30) L2 : (13,10) - (17,45) L3 : (10,0) - (60,25)

   Show all the calculations for Li . Marks in this question will be given if the clipping process and calculations are correct.
   
   Now, assume that the coordinates given in the question are screen coordinates. Give the pixels that should be lighted for each of the clipped Li and Lk at the clip boundaries, if line was generated first and clipped later.

* Improper/incomplete calculations/justifications will not get any credit.

1. Give brief answers for the following -
   
   
   1. Consider a convex polygon with n vertices being clipped against a clip rectangle. What is the maximum no. of vertices in the resulting clipped polygon? What is the minimum number? Justify your answer.
   2. Compare and contrast axonometric orthographic and perspective projections. In other words, in what ways they resemble and what ways they differ?
   3. How are these terms related?
      smooth picture, fine details, pixel dot size, inter-dot distance, resolution
   4. Compare and contrast two different types of shadow-mask CRTs wrt sharpness of image and electron-guns alignment.
   5. Justify true/false - "Sutherland-Hodgman polygon clipping algorithm works only for convex clipping regions".
2. A raster scan of N lines with M pixels per line displayed at R cycles per second has horizontal retrace time Th microseconds and vertical retrace time Tv microseconds. Derive the expressions for computing percentage of time that no image is being traced and use them to compute this time for the given set of values.
   
   

   M X N	R	Interlace	Tv	Th
   640 X 485	30	yes	1271	11
   640 X 485	60	no	1250	7

   
   What is the meaning of the percentages that you have calculated?
3. Brain twisters : Good answers may get more than 100% marks.
   
   
   1. Suppose we are interested in generating stereo-pairs (two views of same scene as seen by humans with both functioning eyes). Can the standard 3D viewing pipeline (as discussed in class) be used for above task? In what way? How?
   2. We want to achieve fade-in fade-out effect (lap-dissolve) b/w two images. Suggest efficient way for doing this. Give relevant details/steps involved in it.
   3. The matrix Mper that we discussed in class, does it define only one point perspective projection? Justify your answer. If your answer to above question is yes, then show how will you get the perspective projection matrix for two/three point perspective projection.
4. In homework no. 1 you were asked to implement Pitteway-Watkinson technique to draw antialiased straight lines. This COMPULSORY question deals with the same homework.
   
   Consider the non-overlapping square pixels of unit size each, centered at the grid points. A unit thickness line is drawn from grid point (1,4) to (5,7). Compute the coordinates of all the pixels that will get lighted up for "x = 3" and "x = 4". Also compute the percentage intensity for each lighted pixel. Show all the relevant calculations clearly.

1. Give short answers -
   
   
   1. What is a vanishing point? How many vanishing points can a scene have?
   2. Give the pipeline for each of the following --
      1. Ray tracing
      2. general 3D transformation, from modelling coordinates to final device coordinates.
   3. Give two important reasons, why polygon mesh representing the model should be triangularised.
   4. Which of - Bezier/B-spline surfaces will you use to model the football goalpost net? Justify your answer in terms of what properties of the object governed you choice.
   5. Give Blending function representation for Hermite splines, i.e. give all the Gi and BFi(u) in "P(u) = 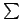(Gi . BFi(u))", where i varies from 0 to 3.
   6. Can the given figure be a projection of a cube? If yes, give a possible plane of projection and a PRP/COP. If no, why not? Assume, no clipping done.
2. Give brief answers -
   
   
   1. A'B' is the parallel projection of the line AB onto some plane. When is the length of A'B' = length of AB?
   2. Diagramatically show the relationship between tints, shades and tones in HSV model.
   3. Why do we need to consider intensity attenuation in our illumination models?
   4. Give the disadvantage of "mapping from texture space to pixel space" as compared to "mapping from pixel space to texture space".
   5. A curve generated with geometric continuity conditions is similar to one generated with parametric continuity, but with a slight difference in curve shape. Explain the difference (answering WHY behind it) with the help of a suitable example.
   6. Compare and contrast between the Ray Casting method and Z-buffer method of visible surface determination.
3. Fill in the blanks -
   
   
   1. CMY are also known as ..... primaries.
   2. If two color sources combine to produce white light, the they are called ..... .
   3. Bezier blending function (Bernstein polynomial) is defined as ..... .
   4. Chromacity = ..... + ..... .
   5. In the HSV model, for pure blue, hue = ..... , value = ..... , saturation = ..... .
4. Give brief answers -
   
   
   1. Give the drawback of Z-buffer that A-buffer improves upon. How?
   2. By looking at the two specular objects kept in the same lighting conditions, can you tell which one has a higher specular exponent (value of n)? How? Why will your method work?
   3. Compare and contrast the two representation schemes for solid objects.
   4. You are modelling a scene containing shiny objects. Which shading model - Phong or Gouraud, will you go for and why?
   5. Is Ray Tracing a view independent algorithm? Justify.
5. Justify true/false -
   
   
   1. B-spline curve will never pass through start and end control points. OR Bezier curve through (10,15) --> (10,20) --> (10,25) will be a straight line". In case you answer true to above, then give the endpoints of this line as well.
   
   
   2. In Phong spcular reflection model, angle between halfway vector and surface normal is always half the angle between reflected ray vector and viewing vector.
6. In Painter's algorithm, when a depth overlap is detected at any point in the list (let current surface being processed in list is S), some additional comparisons/tests are performed in the order of increasing difficulty, to determine whether any of the surfaces should be reordered. If any of the tests is true then no reordering is necessary for the surface S.
   
   Out of these tests, two tests are stated as -
   
   • Surface S is completely behind the overlapping surface relative to the view position.
   • Overlapping surface is completely in front of surface S relative to the view poistion.
   
   There seems to be some mistake here, because both these tests seem identical? Justify your stand with suitable explanations and examples.
7. Compute the perturbed normal for bump-mapping a plane rectangular surface.